Campo Electromagnético
|
Actividad de Aprendizaje: |
Identifica los modelos matemáticos asociados
a diversos elementos generadores de campo electromagnético. |
Basados en la publicación de Oersted, André Marie Ampere por un
lado y Biot y Savart por otro, trataron de explicar
matemáticamente el fenómeno. Proponiendo los segundos investigadores lo
siguiente:
Si por un conductor cualquiera circula una corriente eléctrica,
elementos diferenciales de la longitud del conductor producen, en cualquier punto
del espacio que rodea al conductor, una diferencial de inducción magnética cuya
magnitud está dada por la expresión siguiente:
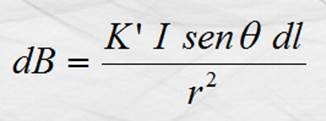
En la que dB es la diferencial de inducción magnética medida en
Tesla; I la corriente eléctrica en el conductor medida en Ampere; r la
distancia del elemento diferencial de longitud
a un punto del campo considerado, medido en metros; K’ la constante de
la ley de Coulomb para el magnetismo; y q el ángulo entre la tangente al
conductor en el elemento diferencial de longitud y la distancia r, medido en
grados. Ver figura.
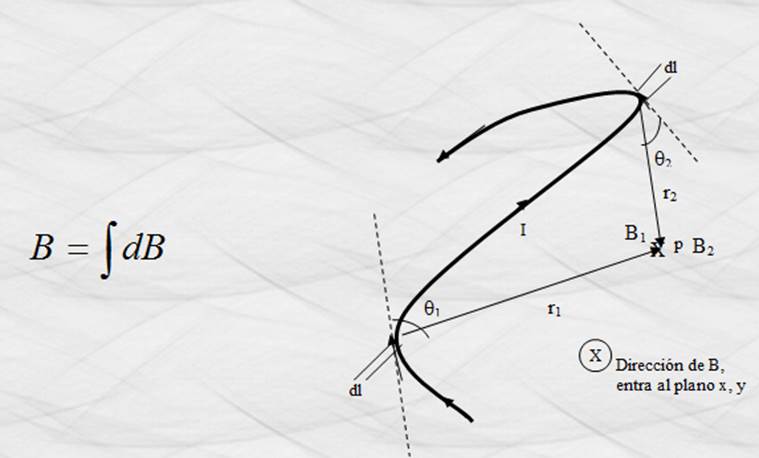
Figura 24. Representación gráfica de la ley de Biot y Savart.
La expresión anterior es lo que conocemos como la ley de Biot y Savart y puede aplicarse a un conductor de forma
cualquiera. A continuación la aplicamos a un conductor de forma recta de
longitud infinita.
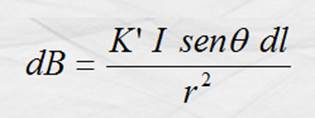
del triángulo
rectángulo formado por x , R y r tenemos:
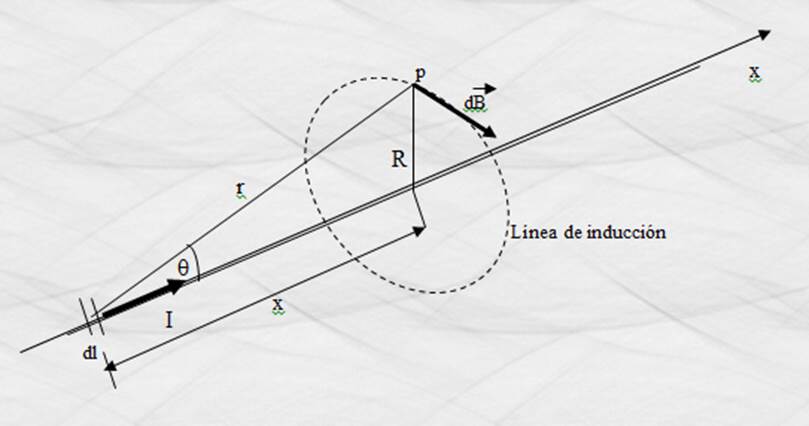
Figura 25.
Representación gráfica de los elementos necesarios para calcular el campo
magnético generado por un alambre recto.
Aplicando
la ley de Biot y Savart
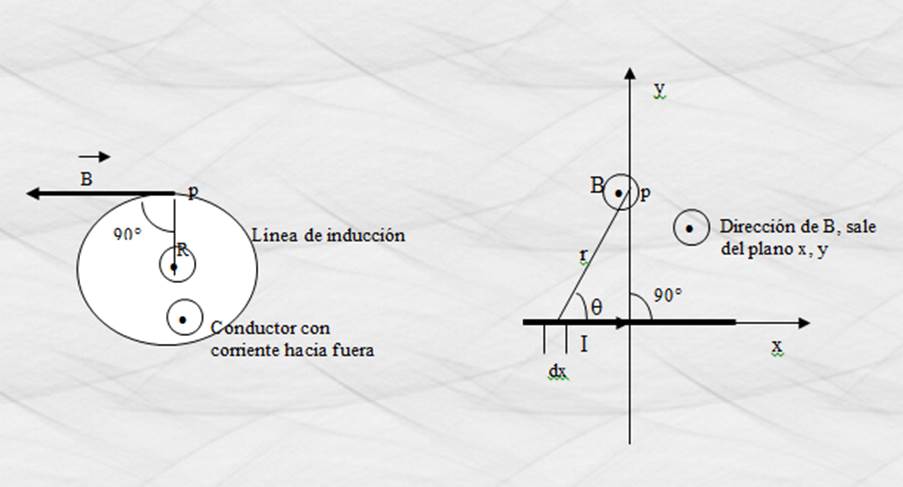
Figura 26.
Representación gráfica de la dirección del campo magnético generado por un
alambre recto.
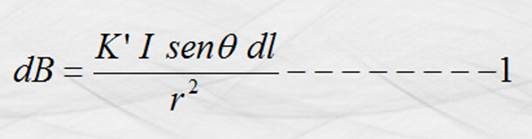
Del triángulo formado en la figura anterior por x, R y r,
tenemos:
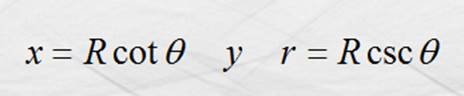
derivando la
primera y elevando al cuadrado la segunda nos queda:
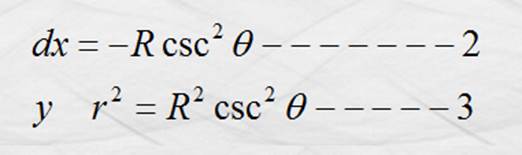
Sustituyendo 2 y 3 en 1 quedamos:
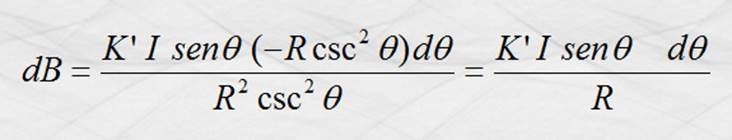
Integrando y tomando como límites q = 0
y q = p.
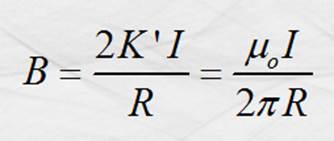
Alambre recto
Esta ecuación representa la herramienta para calcular la
magnitud de la inducción magnética a una distancia R de un conductor de
longitud infinita debida a la corriente en los elementos diferenciales de
longitud del conductor. En la ecuación “B” es la inducción magnética total y
“R” la longitud perpendicular al conductor, que va del conductor al punto
considerado, en metros. Por lo que respecta a la dirección del
vector inducción magnética, ésta puede conocerse aplicando la regla de la mano
derecha, mostrada en la figura siguiente.

Figura 27.
Regla de la mano derecha para calcular la dirección del campo magnético
generado por un alambre recto.
Como se nota, el conductor se envuelve con los dedos de la mano
derecha dejando libre el pulgar, el que indica la dirección convencional de la
corriente. Los dedos representan las
líneas de inducción del campo magnético asociado, formando círculos
concéntricos con el conductor y las uñas
la dirección convencional del campo. Para determinar la dirección del vector inducción magnética en el punto considerado, se
supone que por el punto pasa por la línea de inducción y tangente a esa línea
pasa el vector B.
De manera semejante, se pueden obtener modelos matemáticos para
conductores con otras formas, frecuentemente usados en el estudio del
electromagnetismo, como mostramos en las figuras siguientes.
Inducción magnética en el
centro de una espira circular:
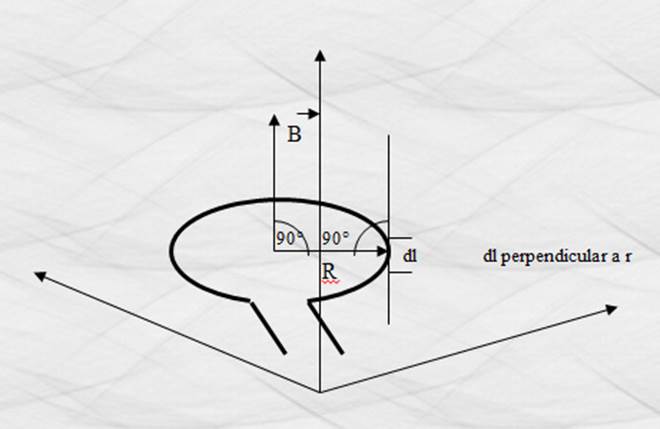
Figura 28. Inducción magnética en el centro de una espira
circular.

Espira Circular
Si la espira la multiplicamos por “n” veces tenemos una bobina
plana y la inducción magnética se multiplica la misma cantidad de veces de modo
que el modelo de la inducción en el centro de la espira circular queda:
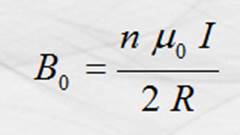
Bobina Circular
Inducción magnética en un
punto del eje de una espira circular:
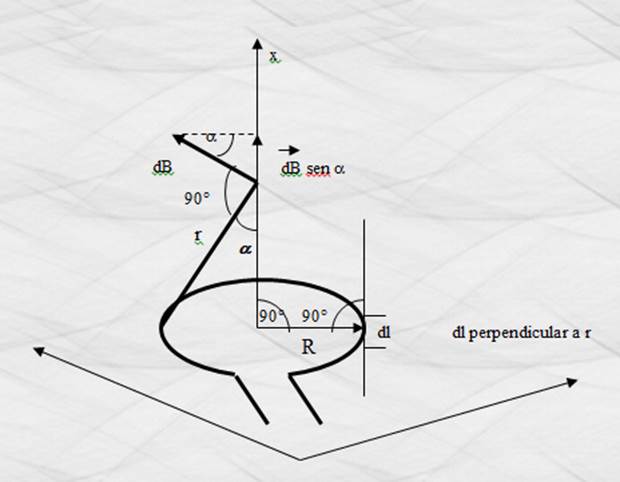
Figura 29. Inducción magnética en un punto del eje de una espira
circular.
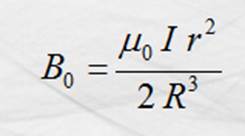
Para una bobina plana solo multiplicamos por “n”:
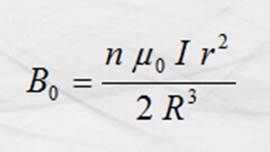
Inducción magnética en el
centro de un solenoide con núcleo de aire:

Figura 30. Inducción magnética en el centro de un solenoide con
núcleo de aire.

Solenoide
donde L es la
longitud del solenoide y “n” el número de vueltas del mismo.
Inducción magnética en el interior
de un toroide con núcleo de aire:
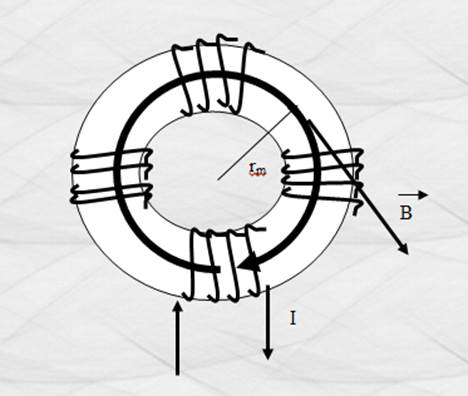
Figura 31. Inducción magnética en el interior de un toroide con
núcleo de aire.
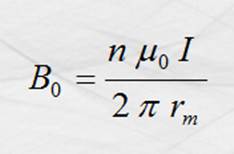
Toroide
![]()
donde “rm “ es el radio medio del toroide .
Nota:
El subíndice cero para todos los
modelos de inducción magnética significa que el medio donde se encuentra el conductor o núcleo es aire;
si se introduce el conductor en otro medio o el núcleo del solenoide se cambia
por otro material, la inducción producida por el conductor con su corriente
correspondiente (por ejemplo, B0)
se debe multiplicar por mr y así obtener la inducción absoluta

En general B = mr B0
Ley circuital
de Ampere:
Andre Marie Ampere por su parte, para conocer la inducción magnética
total debida a elementos diferenciales de longitud que transportaban
la misma corriente y cuyas diferenciales de inducción magnética tenían cierta
simetría, llegó a la siguiente expresión:
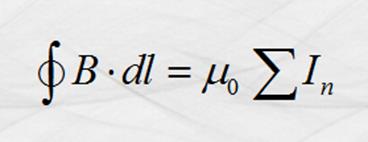
que se puede
enunciar de la manera siguiente:
“La inducción magnética producida por una
corriente o conjunto de corrientes encerradas en una trayectoria hipotética es
igual a la suma algebraica de las corrientes multiplicada por la permeabilidad
del medio en el que se encuentren”
Con el fin de interpretar la simetría mencionada, analicemos la ley
de Ampere, aplicada a un conductor recto de longitud infinita que se muestra a
continuación.
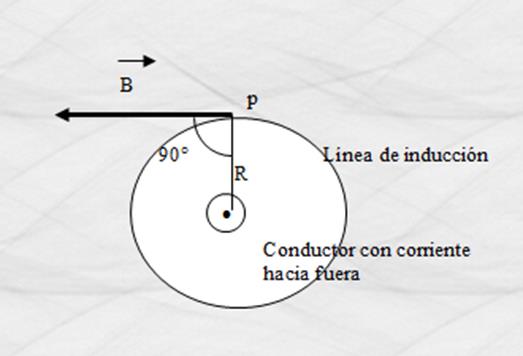
Figura 32. Línea de inducción para un conductor rector.
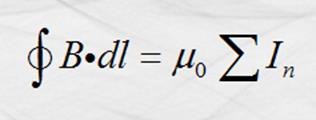
Como n = 1 , ![]() y el ángulo q en B y dl igual a 0°, tenemos:
y el ángulo q en B y dl igual a 0°, tenemos:
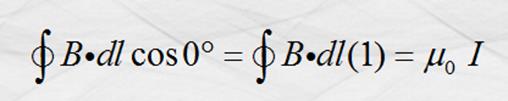
y como B es
constante en magnitud; y ya que todos los elementos diferenciales forman el perímetro
de la circunferencia.
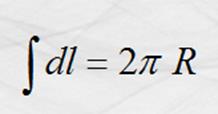
sustituyendo y despejando B tenemos:
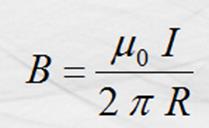
este último
modelo es semejante al que se obtuvo aplicando al mismo conductor la ley de
Biot y Savart.
Esta ley se puede aplicar a otra forma de conductores como las
vistas anteriormente y llegar a los mismos resultados obtenidos con la ley de
Biot y Savart. Su aplicación se recomienda para cuando haya simetría entre las
inducciones diferenciales; si no la hay, su aplicación será más compleja que
aplicar la ley de Biot y Savart.