Fuerza de Lorentz
|
Actividad de Aprendizaje: |
Interpreta la aparición de una fuerza
magnética sobre una partícula cargada eléctricamente dentro de un campo
magnético. |
Si colocamos un imán, suspendido libremente, en un punto dentro del
campo magnético de otro imán o dentro de cualquier otro campo magnético, el
primer imán girará rápido o lento para alinearse con el campo del segundo; la
rapidez de giro depende de la intensidad de la inducción magnética del campo y
de la masa magnética del primer imán. De esta forma podemos detectar un campo
magnético en un punto; otra forma de hacerlo es colocando en el campo una carga
eléctrica en movimiento, la desviación de la trayectoria de la carga indicará
la presencia de un campo.
Lo escrito anteriormente, indica que si una carga en movimiento
penetra en un campo magnético, se acelerará debido a una fuerza de origen
magnético, esto fue descubierto por Hendrik A. Lorentz, quien propuso que la fuerza resultaba del producto
vectorial de los vectores v y B
relacionados en la ecuación:
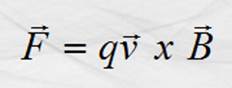
Como F es una cantidad vectorial, su magnitud se calcula con la
expresión:
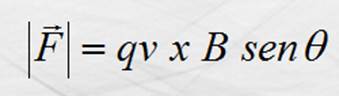
En la que q es el ángulo entre v y B. Atención entre v y B no entre B y v.
La dirección de F es la de
la línea perpendicular al plano que contiene los vectores velocidad e inducción
magnética o normal, saliendo o entrando al plano de acuerdo con la regla de la
mano izquierda o del tornillo de cuerda derecha. Ver figura siguiente.

Figura 33.
Regla de la mano izquierda para determinar la dirección de la fuerza magnética.
Esta regla es aplicable al caso de cargas eléctricas positivas
en movimiento. Si las cargas son negativas, para conocer la dirección, se
emplea la regla de la mano derecha, con denominación idéntica para los dedos.
Si la carga que se introduce en el campo es positiva, posee una
velocidad constante ( M. R. U. ) y entra
perpendicularmente al campo, la trayectoria descrita por la carga dentro del
campo es un circulo. Esto es debido a que la fuerza de Lorentz
que actúa permanentemente sobre la carga es de magnitud constante y siempre
dirigida al centro de la trayectoria. Ver la figura siguiente.
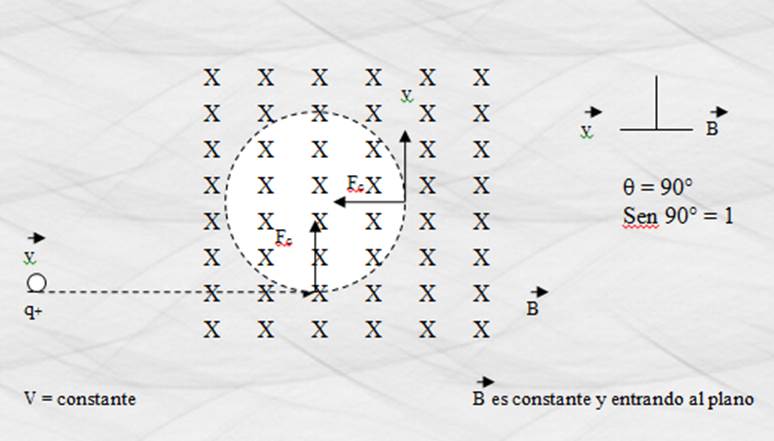
Figura 34. Movimiento de una carga eléctrica dentro de un campo
magnético.
Fuera del campo magnético, la carga tiene un M.R.U. y dentro un
M.C.U.
Como la trayectoria es circular y la rapidez de la carga constante,
el Movimiento es Circular Uniforme de radio R; fuerza centrípeta, Fc ; rapidez
constante, v ; frecuencia, f y período , T ; todos constantes.
Haciendo un análisis de este movimiento, podemos obtener de la
manera siguiente, un conjunto de ecuaciones que lo describen, comenzando con R.
Como
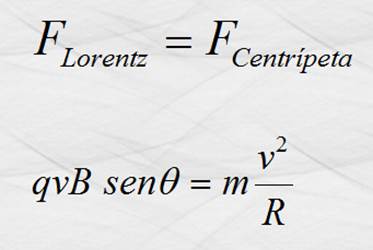
Y ya que q = 90° ; sen
90° = 1
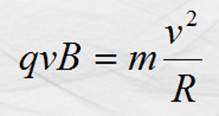
Despejando a R
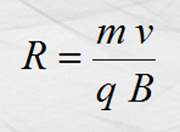
Continuando con el período T y la frecuencia f:
Despejando v de la ecuación del radio
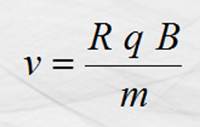
Y también de la ecuación
que relaciona a y T del M. C. U.
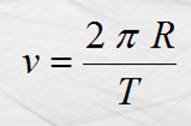
Igualando las ecuaciones anteriores y despejando T:
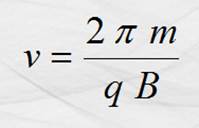
Y ya que
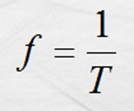
entonces:
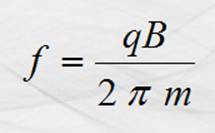
Y como la carga está en movimiento, posee una energía
cinemática:
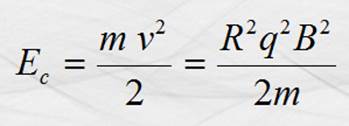
Detalles del ángulo entre v y
B.
Si el ángulo es 0°, no
hay fuerza de Lorentz sobre la carga y se moverá
paralela a las líneas de inducción del campo en el que penetra.
La fuerza de Lorentz es un concepto
que se usa como parte fundamental en la construcción de máquinas como el
Ciclotrón o el espectrómetro de masas,
útiles en el estudio de la Física Moderna. Ver “Física General”, Sears- Zemansky ,
ED. Aguilar.
Si la carga penetra en el campo formando un ángulo q diferente de 90° y 0° con las líneas de inducción del campo, en
lugar de tener las trayectorias anteriores, ésta será una combinación de las
dos, una espiral, ya que la componente de la velocidad perpendicular al campo
obligará a la partícula a tener una trayectoria circular, en un plano
perpendicular al campo; y la componente de la velocidad paralela al campo
obligará a que la partícula se desplace paralela al campo con velocidad
constante.
Es común hablar de un conjunto de cargas, haz, en lugar de
solamente una, mientras éstas se muevan libremente, se comportarán de igual
forma que una.
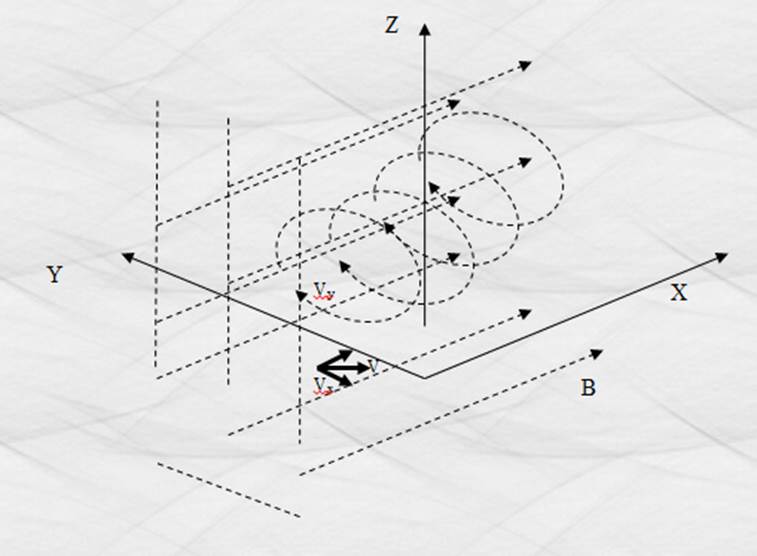
Figura 35. Haz de electrones dentro de un campo magnético.
En el dibujo, B está atravesando perpendicularmente el plano “YZ”, perpendicular al eje x. La
carga se mueve en el plano “XY” teniendo su velocidad dos componentes: Vx
, paralela al eje “x” que hace que la carga avance con velocidad
constante a lo largo del eje ”x” ; y Vy,
paralela al eje “ye” y al interaccionar con B hace que la carga describa una
trayectoria circula en el plano “YZ” . La suma de los desplazamientos en ambas
direcciones da como resultado una trayectoria espiral.