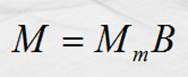Momento de Torsión Magnético
|
Actividad de Aprendizaje: |
Distingue entre momento de torsión magnético
y momento magnético. |
Si en lugar de hacer circular la corriente por un conductor
recto, la hacemos circular por una espira como la mostrada en la figura, y esta
espira la suspendemos de manera que pueda girar, tendremos físicamente, un
motor de una sola espira que sólo oscilara, no girará debido a su disposición
mecánica.

Figura 37. Espira con corriente dentro de un campo magnético.
Explicar el giro de la espira es relativamente sencillo.
Aplicando la regla de la mano izquierda a los segmentos ab y cd deducimos la
dirección de las fuerzas mostradas en la figura, cada fuerza con la intensidad
siguiente:
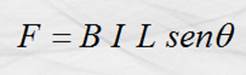
Como ambas fuerzas son iguales en magnitud y dirección contraria
y están aplicadas a la misma distancia del eje de giro, tenemos físicamente un
par de fuerzas cuyo momento es:
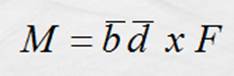
o
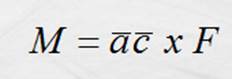
sustituyendo el equivalente de F
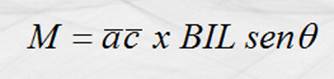
donde ac o bd es la distancia
perpendicular a las líneas de acción de ambas fuerzas y puesto que para cada posición de la bobina q = 90ª y sen 90º =1 tenemos:
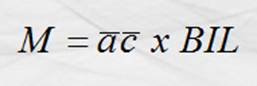
Por otro lado, geométricamente a c x L = A; donde A es el área
de la espira medida en metros cuadrados, de modo que sustituyendo el área
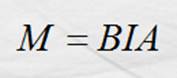
ecuación que
corresponde al momento mecánico máximo de la espira.
Ahora, consideremos en lugar de una espira, un conjunto de estas
formando una bobina plana de “n” espiras. La magnitud del momento máximo se
representa por la ecuación siguiente:
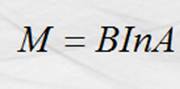
Momento mecánico variable de
una bobina con corriente dentro de un campo magnético:
Por comodidad obtuvimos el momento mecánico máximo de la bobina,
aunque el torque varía para cada posición de la bobina durante una vuelta, ya que
el ángulo entre la dirección de la fuerza y las líneas de inducción varía
continuamente.
Como la componente de la fuerza que produce el giro cambia de magnitud en función de la posición
de la bobina, propondremos una ecuación nueva para calcular el momento mecánico
de la bobina en función de su posición y es la siguiente:
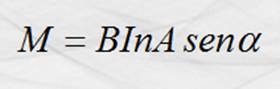
en la que a es el ángulo que forman : un vector área imaginario A , perpendicular a el plano de la
bobina y el vector inducción magnética B.
Considerado de esta forma, el momento tiene un valor máximo cuando a = 90º ; tiene un valor entre 0 < M < B I n A para
cualquier ángulo entre 0 < a < 90º respecto a la horizontal y valdrá cero para a = 0, como se ilustra en las figuras
siguientes.
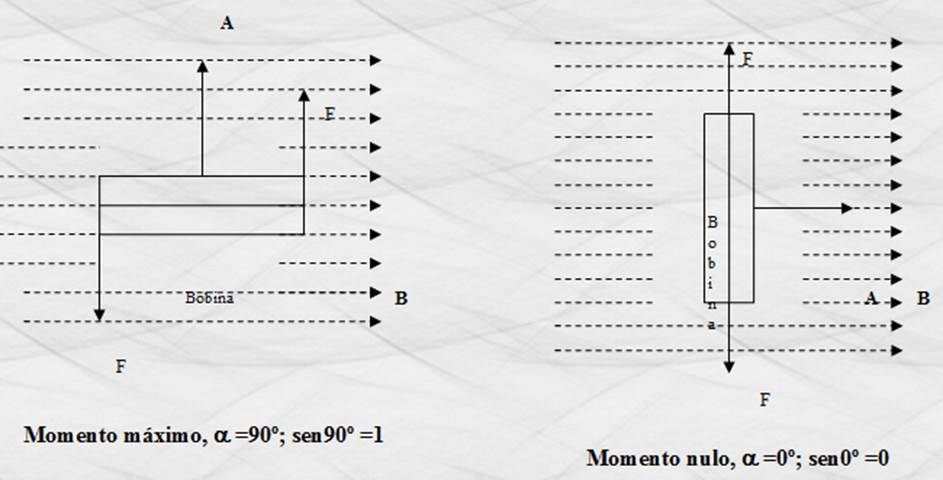
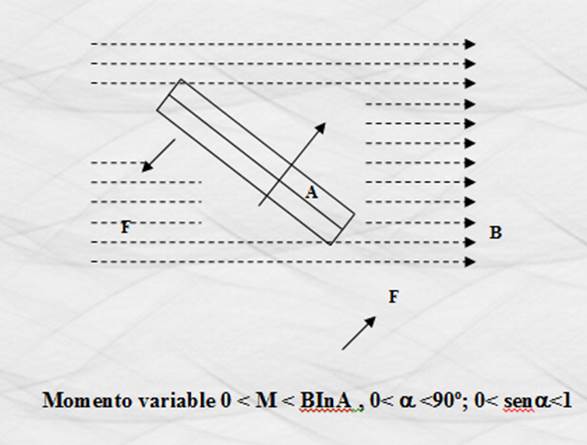
Figura 38. Momento mecánico en función del ángulo
a.
Momento magnético:
El momento mecánico de la bobina, puede decirse, es debido a la
interacción de dos campos magnéticos, uno es el campo en el que se encuentra la
bobina y el otro , el de la bobina con corriente , n I
, este último podemos asociarlo con una cantidad física característica de la
bobina con corriente, denominada momento magnético. El momento magnético lo
definimos como la razón del momento mecánico entre la inducción del campo donde
se encuentra la bobina.

Considerado de esta
forma, el momento mecánico es igual a: