Leyes de la Reflexión y Espejos
|
Actividad de Aprendizaje: |
Aplica las leyes de la
reflexión para determinar las características de las imágenes que se forman
en espejos planos y esféricos. |
Cuando los fenómenos poseen semejanzas se
agrupan en una parte de la ciencia, recibiendo el agrupamiento un nombre
particular. Tal es el caso de los fenómenos relacionados con la luz que
agrupados reciben el nombre de fenómenos ópticos u óptica.
La óptica, a su vez, para facilitar su
estudio se subdivide en Óptica Geométrica
y Óptica Física. La primera estudia
los fenómenos relacionados con la propagación rectilínea de la luz como la
reflexión y refracción de la luz y la segunda los relacionados con
características propias de las ondas como la difracción, la interferencia, la
polarización, la dispersión, la absorción, etc.
Continuaremos nuestro estudio con la
reflexión de la luz en espejos planos y esféricos; no trataremos los espejos
cilíndricos ni parabólicos.
Espejo es una
superficie pulida que refleja especularmente un rayo de luz incidente.
Por lo que respecta a la reflexión de la
luz, esta puede ser especular o difusa;
es especular si un rayo incidiendo oblicuamente en un obstáculo rebota
regresando a su medio de propagación sin dividirse y en una dirección
determinada por las leyes de la reflexión, descritas con anterioridad; por otro
lado, la reflexión es difusa si el rayo al incidir en un obstáculo se parte
resultando rayos en direcciones diferentes. Ver ilustración:

Figura 107. Reflexión especular y reflexión difusa.
Ahora, definamos algunos términos para el
estudio de la reflexión.
Objeto: Es un
cuerpo físico que se coloca enfrente de un espejo para reflejarlo. Puede ser
luminoso o iluminado; el primero tiene luz propia, ejemplo: El sol, una
lámpara, una antorcha, un cuerpo muy caliente, etc.; los segundos no tiene luz
propia y puede ser cualquier otro cuerpo; los iluminados los clasificamos en:
Transparentes: son
aquellos que permiten el paso de la luz a través de ellos y se pueden observar
otros objetos dentro o detrás de ellos, ejemplo: el agua, el vidrio, algunos
aceites, algunos polímeros, etc.
Translucidos:
Permiten el paso de la luz a través de ellos, pero un objeto colocado detrás de
ellos, no ve bien definido, solo se
aprecia su volumen, ejemplo vidrios opacos, algunos polímeros y aceites.
Opacos: No
permiten el paso de la luz ocasionando sombras cuando son iluminados, ejemplo
de estos, la mayor parte de cuerpos físicos.
Imagen: Es la
reproducción visual de un objeto, obtenida por reflexión o refracción de la
luz. La imagen obtenida por reflexión de la luz puede ser real o virtual; es real si se forma con rayos reflejados, es
virtual si se forma con prolongación de rayos reflejados o detrás de un espejo.
La imagen puede ser derecha o invertida; si se forma arriba del eje focal del espejo es derecha; si se forma debajo es
invertida. La imagen también puede ser ampliada, si su altura es mayor que la
altura del objeto y reducida al revés.
Rayo: Es una
línea recta perpendicular al frente de onda plana; un conjunto de rayos forman
un haz. El rayo es un concepto más útil que el frente de onda, en el estudio de
la reflexión y refracción de la luz.
Reflexión de la Luz En Espejos Planos
Espejo plano es una superficie pulida de
radio de curvatura infinito (plana) en la que un rayo se refleja
especularmente.
Cuando se coloca un objeto frente a un
espejo plano, en este ultimo se observará una imagen
del objeto con las características siguientes:
Virtual, derecha, simétrica respecto al
plano del espejo, y del mismo tamaño del objeto. A continuación se ilustra el
párrafo:

Figura 108. Imagen virtual en un espejo plano.
Espejo Diedro
El espejo diedro está compuesto de dos
espejos planos unidos por una de sus aristas. La abertura, a,
entre las superficies puede ser de

Figura 109. Espejo diedro.
Reflexión de la Luz en Espejos Esféricos
Un espejo esférico es un casquete de esfera
hueca pulida interior o exteriormente. Si el casquete está pulido internamente,
el espejo se denomina cóncavo, si lo está exteriormente se llama convexo.
Los espejos esféricos forman imágenes de
todos tipos, virtuales, reales, derechas, invertidas, ampliadas y reducidas;
éstas dependerán del espejo seleccionado y de la distancia del objeto al
vértice del espejo.
Se pueden determinar las imágenes de dos formas:
geométrica y analíticamente.
Para determinar las imágenes, escribamos
algunas definiciones útiles.
Eje principal: Es una
línea recta imaginaria que parte horizontalmente al espejo en dos. En él
están localizados el vértice, el foco y
el centro.
Vértice: Es el
punto de interacción del espejo y el eje focal, abreviado v.
Foco: Es un
punto en el eje focal de un espejo cóncavo, donde concurren los rayos
reflejados en éste, que inciden paralelos al eje. En el espejo convexo, es un
punto en su eje focal donde, aparentemente, surgen los rayos reflejados en la
superficie del espejo, que inciden paralelos al eje de este. El foco en el
espejo cóncavo es real y en el convexo es virtual; algebraicamente, la
distancia focal del espejo cóncavo es
positiva y la del convexo es negativa.
Centro del espejo: Es un punto en el eje focal correspondiente al centro de la esfera de
donde se obtuvo el espejo, se abrevia “c”.
Radio: Es el
radio de curvatura de la esfera, corresponde con la distancia del centro de la esfera al
vértice, se abrevia “R”. Algebraicamente, esta distancia es positiva para espejos cóncavos y negativa para convexos.
Distancia focal: Es la longitud del segmento de recta que une al vértice y el foco, se
abrevia “f”. Algebraicamente, “f” es positiva (real) para espejos cóncavos y
negativa (virtual) para los convexos.
Geométricamente, para espejos esféricos, f = R/2.
Distancia del objeto al espejo: Es la longitud del segmento de recta entre el punto
donde se coloca el objeto frente al espejo y el vértice. Se simboliza con “p“.
Distancia de la imagen al espejo: Es la longitud del segmento de recta que une el vértice
del espejo y el punto donde se localiza al imagen. Su
símbolo es “q” y es “+q” para imágenes reales y “–q”
para virtuales.
Altura del objeto: Es la longitud del tamaño del objeto, se abrevia “O”.
Altura de la imagen: es la longitud del tamaño de la imagen, se abrevia “I”.
Ampliación Lateral: Es la razón en valores absolutos de “q” entre “p” o “ I
“ entre “O”; se abrevia “M”.

Figura 110. Espejo cóncavo.

Figura 111. Espejo convexo.
Formación de Imágenes en Espejos Esféricos
Formar imágenes de objetos en espejos
esféricos teóricamente, es seguir un proceso que requiere conocer lo que son
los rayos notables o principales. Los rayos principales son tres, se describen
a continuación e ilustran.
1.-Los rayos paralelos al eje de un espejo
cóncavo, provenientes de un objeto en el infinito, que incidan en éste, se
reflejan pasando por su foco. En el caso del convexo, se reflejan en forma tal
que parecen provenir del foco.

Figura 112. Reflexión de rayos paralelos en espejos esféricos.
2.- Los rayos que pasan por el foco de un
espejo cóncavo se reflejan paralelamente al eje; en el caso del convexo , los rayos no pueden pasar por el foco pero si se
pueden prolongar de tal manera que los rayos reflejados parecieran provenir del
foco.

Figura 113. Reflexión de rayos incidentes que pasan por el foco en espejos esféricos.
3.- Todo rayo que pase por el centro de un
espejo cóncavo o parezca provenir de un espejo convexo, se reflejará 180°
desviada de la dirección de incidencia. Es decir el rayo incidente y el
reflejado son colineales y desviados 180°.

Figura 114. Reflexión de rayos incidentes que pasan por el centro en espejos esféricos.
El proceso citado, consiste en trazar los
rayos notables en un dibujo del espejo a escala, localizando el punto donde se
cruzan tales rayos, en éste se localiza la imanen, a continuación se ilustra el
procedimiento.

Figura 115. Rayos principales en espejo cóncavo.

Figura 116. Rayos principales en espejo convexo.
Los espejos cóncavos pueden forman todo
tipo de imágenes: reales y virtuales; derechas e invertidas; ampliadas y
reducidas. En cambio los espejos convexos solo producen imágenes virtuales,
derechas y reducidas.
Para que los espejos cóncavos produzcan
imágenes diferentes, se requiere colocar el objeto a distancias diferentes
respecto al vértice, el foco y el centro del espejo.
Si el objeto se coloca lejos, mas allá del
centro, a partir del vértice, la imagen será real, invertida y reducida.
Si acercando el objeto lo colocamos en el
centro del espejo, la imagen será real invertida y del mismo tamaño que el
objeto.

Figura 117. Objeto colocado en el centro de un espejo cóncavo, y su imagen.
Si acercando el objeto lo colocamos entre
el centro del espejo y el foco, la imagen será real invertida y de mayor tamaño
que el objeto, ampliada.

Figura 118. Objeto colocado entre el centro y el foco de un espejo cóncavo, y su imagen.
Si acercando el objeto lo colocamos en el
foco del espejo, la imagen no se forma porque los rayos reflejados no se
cruzan.

Figura 119. Un objeto colocado en el foco de un espejo cóncavo no pruduce imagen.
Si acercando el objeto lo colocamos entre
el foco del espejo y el vértice, la imagen será virtual, derecha, y de mayor tamaño que el objeto,
ampliada.

Figura 120. Objeto colocado entre el foco y el vértice de un espejo cóncavo, y su imagen.
Como ya vimos, cuando tratamos los rayos
principales, los espejos convexos forman imágenes virtuales, ahora alejemos el
objeto del vértice y obtengamos de nuevo una imagen virtual, derecha y reducida.

Figura 121. Objeto colocado frente a un espejo convexo, y su imagen.
Ya que la localización de la imagen se
realizo a escala, su posición se obtiene midiendo la distancia “q” y su
ampliación o reducción, midiéndola también.
Otra forma de determinar la posición de la
imagen de un objeto es usando la ecuación deducida por Frederick Gauss que se establece
como sigue:
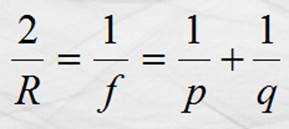
Y se deduce geométricamente como sigue:

Figura 122. Esta imagen apoya la deducción de la ecuación de Gauss para espejos.
Del triángulo o c p .
 porque el ángulo suplementario de un ángulo en un triángulo
es igual a la suma de los ángulos internos no suplementarios.
porque el ángulo suplementario de un ángulo en un triángulo
es igual a la suma de los ángulos internos no suplementarios.
Del triángulo OIP
![]() por la razón anterior.
por la razón anterior.
Despejando a q de (1), sustituyendo en (2) y
simplificando tenemos:
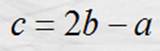
Reacomodando:

Y como para ángulos pequeños, la tangente
de un ángulo es igual al valor del ángulo expresado en radianes,
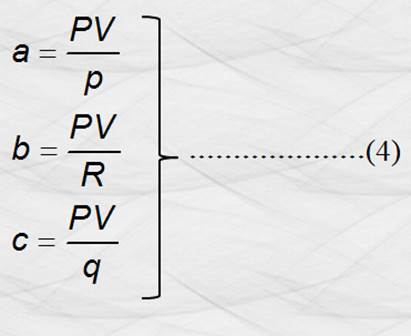
Sustituyendo las ecuaciones (4) en (1) tenemos:
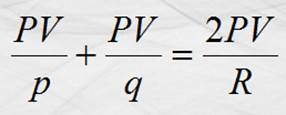
Dividiendo entre PV

Donde las distancias se miden en metros
para el S. I. ; “R” y “f “ son positivas para espejos
cóncavos y negativas para convexos; “q” es positiva para imágenes reales y
negativa para virtuales y “p” siempre positiva.
Para obtener la ampliación lateral o
reducción de la imagen hacemos uso del modelo siguiente:
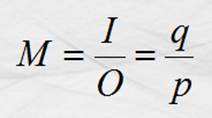
Donde I es la altura de la imagen en
metros; O la altura de el objeto en metros; y M, la ampliación o reducción,
adimensional.
En la siguiente animación interactiva
podrás verificar las características de las imágenes que se producen en espejos
cóncavos y convexos; sólo arrastra el objeto (la vela) a la posición que desees y
selecciona el tipo de espejo: cóncavo (concave mirror) o covexo
(convex mirror).