Leyes de la Refracción y Lentes
|
Actividad de Aprendizaje: |
Aplica las leyes de la refracción
para determinar las características de las imágenes que se forman en lentes convergentes
y divergentes. |
Cuando un rayo de luz incide oblicuamente
en la interfase de dos medios y continua propagándose en el segundo medio, su
dirección nueva se acerca o aleja de la normal
(N).
Como ya
lo discutimos al analizar el movimiento ondulatorio, este fenómeno se conoce como refracción de una
onda.

Figura 123. Refracción de la luz.
El cambio geométrico de dirección se
manifiesta mecánicamente como una variación de la rapidez de la luz al cambiar
de medio de propagación, conservándose la frecuencia y variando la longitud de
onda. Este comportamiento es debido a una propiedad de la materia que
asociaremos con el índice de refracción de un material, abreviado “n”.
Como el índice de refracción asocia dos rapideces y dos medios, el índice
de refracción de un medio lo referiremos al otro, definiéndolo como la razón de
las velocidades con que se propaga la luz en ambos. El medio de la referencia
común es el vacío. Matemáticamente:
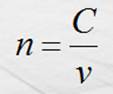
Donde C es la rapidez de la luz en el
vacío, en m/s; v la rapidez de la luz en el medio, en m/s; y n el índice de
refracción medio, referido al vacío, adimensional.
Como la referencia, al definir el índice de
refracción es el vacío, el índice de
refracción para éste es uno y prácticamente, como la rapidez de la luz tiene el
mismo valor para el vacío. El índice de refracción para el aire también es uno.
En el estudio de la refracción hay dos
leyes que nos auxilian en la explicación de los fenómenos, éstas son:
1a.- El rayo incidente, el rayo
refractado y la normal están en un mismo plano. Esto es semejante a la primera
ley de la reflexión.
2ª.- La trayectoria de un rayo refractado en la interfase
de dos medios es exactamente reversible; esto quiere decir, como lo muestra la
figura anterior, que si el rayo pasa de un medio primero a un segundo medio de
mayor índice de refracción, se acercará a
Ley de Snell
Willebrord Snell dedujo geométricamente una forma de
conocer el índice de refracción de un medio, haciendo uso de la desviación de
un rayo oblicuo al cambiar de medio de propagación. El modelo matemático al que
llegó recibe el nombre de Ley de Snell.
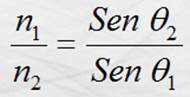
Y se deduce como sigue:

Figura 124. Esta imagen apoya la deducción de la ley de Snell.
De acuerdo con la figura anterior v1
> v2, para los triángulos ABD Y ACD, la hipotenusa es la misma
(distancia AD). La distancia recorrida por el rayo en el medio segundo es AC =
v2t y la recorrida por el
rayo paralelo en el medio primero es BD = v1t para el mismo tiempo.
De los dos triángulos rectángulos mencionados obtenemos:

Dividiendo ambas ecuaciones:
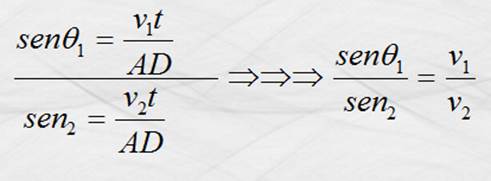
En la que q1 es el ángulo de incidencia; q2, el ángulo de refracción, medidos respecto
a la normal; n1 el índice de refracción del medio en el que se
propaga la onda; y n2 el índice del medio en el que se introduce. La
ley de Snell puede presentarse en base a la rapidez de propagación en los
medios ó la longitud de onda de los rayos, como se muestra a continuación:

Si n1 es un índice de refracción
incógnita, aplicando la ley de Snell tenemos:
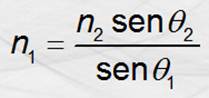
Cuando un rayo que se propaga en un medio
incide oblicuamente sobre otro, cuyo índice de refracción es mayor, el rayo
refractado se desvía acercándose a

Figura 125. Refracción de la luz en un medio con mayor índice de refracción.

Figura 126. Refracción de la luz en un medio con menor índice de refracción.
Ángulo Crítico o Ángulo Límite
No siempre que un rayo de luz pasa oblicuamente
de un medio a otro de densidad menor se refracta, en este fenómeno hay un
ángulo de incidencia para el cual el rayo refractado es máximo, es decir el
ángulo de refracción es p/2 radianes (90º); para un ángulo de
incidencia mayor que el crítico, el rayo no pasa al otro medio y se refleja. El
ángulo crítico se puede calcular de una ecuación derivada de la ley de Snell y
es la siguiente:
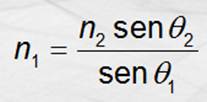
Si n2 > n1 y qc = q1 es el ángulo de incidencia crítico, sen q2 = sen qr = sen 90° = 1,
de modo que sustituyendo lo anterior:
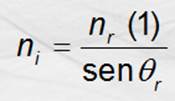
Despejando qc:
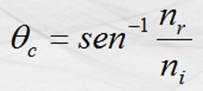

Figura 127. Esta imagen apoya la deducción del ángulo crítico.
En la figura anterior, el medio 2 tiene un
índice de refracción mayor que el medio 1 (n2
> n1). El rayo 1 incide en la interfase a un ángulo q1 menor que el ángulo crítico y se refracta
alejándose de la normal. El rayo 2 incide en la interfase al ángulo crítico o ángulo
límite y se refracta alejándose lo
máximo de
Refracción de la Luz en Lentes Delgadas
Las lentes son dispositivos capaces de
ampliar la imagen de un objeto, para observarlo con detalle o proyectarlo en
una pantalla. Las lentes delgadas forman parte de una cámara fotográfica,
prismático, proyector de película, microscopios, telescopios, etc.
La formación de una imagen con una lente
delgada se basa en la refracción de la luz cuando un rayo luminoso atraviesa un
medio refringente; se le llama lente delgada porque sus dimensiones son grandes
en comparación con su espesor.
Las lentes son cuerpos transparentes que
refractan los rayos de luz cuando inciden en ellos; pueden ser convergentes o divergentes. Las
lentes convergentes son: biconvexa, plano-convexa y menisco- convergente; dos
de sus características generales es que son gruesas en el centro y delgadas en
las orillas y convergen a un foco los rayos que inciden paralelos al eje de la
lente. Las lentes divergentes son: bicóncavas, plano-cóncavas y
menisco-divergentes; son delgadas en el centro y gruesas en los extremos; y
divergen los rayos que inciden paralelos al eje de la lente, como si los rayos
divergidos provinieran de uno de los focos de la lente.

Figura 128. Lentes convergentes.

Figura 129. Lentes divergentes.
Las lentes tienen un eje focal semejante al
eje de los espejos, donde se localizan dos focos en lugar de uno y dos centros
que pueden ser simétricos o asimétricos respecto al centro de lente, ya que los
radios de curvatura de cada superficie de la lente pueden ser iguales o no. Por
lo que respecta a la localización de los focos simétricos, la longitud no es la
mitad del radio de curvatura como en los espejos esféricos, medida desde el centro,
sino se calcula en función del índice de refracción del material y los radios
de curvatura de las superficies de incidencia, con la ecuación de los pulidores
de lentes que es la siguiente:

En la que obvio, es f la longitud focal,
medida desde el centro de la lente, en metros; R1, el radio de
curvatura de la superficie 1, media en metros;
R2, el radio de curvatura de la superficie 2, media en
metros; y n el índice de refracción del
material de la lente.
Para obtener, geométricamente, imágenes
formadas por lentes convergentes, haremos uso de los rayos principales
siguientes:
1.- Todo rayo, proveniente del objeto,
paralelo al eje focal que incide en la lente, se refracta pasando por el foco
después de la lente.

Figura 130. Refracción de rayos paralelos en una lente convergente.
2.- Todo rayo, proveniente del objeto, que
pasa por el foco anterior de la lente,
se refracta paralelo al eje focal.

Figura 131. Refracción de rayos provenientes del foco en una lente convergente.
3.- Todo rayo que atraviesa el centro de la
lente no se refracta.
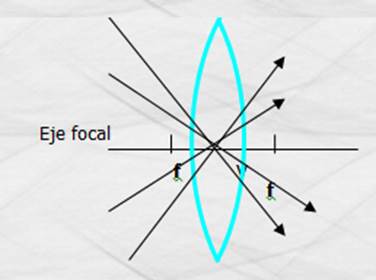
Figura 132. Refracción de rayos que atraviezan el centro de una lente convergente.
Formación de una imagen con rayos
principales que inciden en una lente convergente.

Figura 133. Rayos principales en una lente convergente.
Para obtener, geométricamente, imágenes
formadas por lentes divergentes, haremos uso de los rayos principales
siguientes:
1.- Todo rayo, proveniente del objeto,
paralelo al eje focal que incide en la lente, se refracta de tal forma que
parezca que viene del foco anterior de la lente.

Figura 134. Refracción de rayos paralelos en una lente divergente.
2.- Todo rayo, proveniente del objeto, que
aparentemente pasa por el foco posterior de la lente, se refracta paralelo al eje focal.
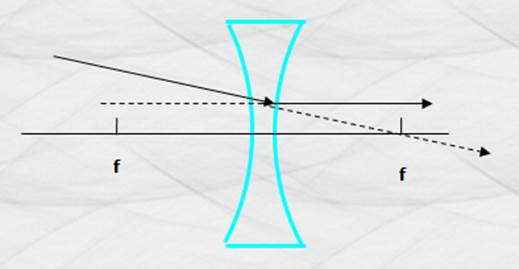
Figura 135. Refracción de rayos que tienden a pasar por el foco en una lente divergente.
3.- Todo rayo que atraviesa el centro de la
lente no se refracta.
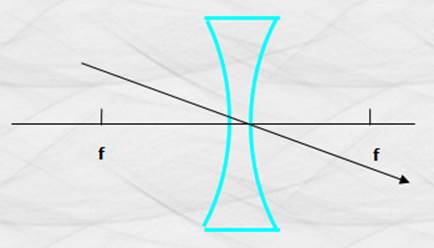
Figura 136. Refracción de rayos que atraviezan el centro de una lente divergente.
Formación de una imagen con rayos
principales que inciden en una lente convergente.

Figura 137. Rayos principales en una lente divergente.
En cuanto al cálculo de la posición de la
imagen, conociendo la posición del objeto y la localización de los focos, se
puede realizar con la ley de Gauss para los espejos. La ampliación lateral se
calcula también con la ecuación correspondiente para los espejos.
Las distancias “p” y “q” significan lo
mismo. En cuanto a los signos de “f” y “r” al aplicar la ecuación de Gauss, serán positivos para
lentes convergentes y negativos para
divergentes. Aquí, los objetos y las imágenes son reales y virtuales,
por lo que los signos correspondientes serán: positivos para los reales y
negativos para los virtuales.
Las imágenes formadas con lentes
divergentes son siempre virtuales, derechas y reducidas.

Figura 138. Imagen formada por una lente divergente.
Por lo que respecta a las generadas por
lentes convergentes, serán variadas y dependerán de la posición del objeto al
centro de la lente.

Figura 139. Objeto colocado más allá del centro de una lente convergente, y su imagen.

Figura 140. Objeto colocado en el centro de una lente convergente, y su imagen.

Figura 141. Un objeto colocado en el foco de una lente convergente no produce imagen.

Figura 142. Objeto colocado entre el foco y el vértice de una lente convergente, y su imagen.