Movimiento Ondulatorio
|
Actividad de Aprendizaje: |
Identifica las
características principales de una onda. |
El movimiento ondulatorio, al igual que
otros movimientos, se presenta en la naturaleza o puede ser producto de un
dispositivo desarrollado por el hombre. Ejemplos de este movimiento son:
En la naturaleza: Las mareas, algunos los
terremotos, la luz solar, algunos sonidos, etc.
Y de los producidos por el hombre: Las
ondas de radio; algunas ondas sonoras en: columnas de aire, cuerdas sonoras o
membranas; el rayo laser, los sintetizadores, generadores de sonido y
ultrasonido, etc.
El movimiento ondulatorio puede ser
perjudicial o benéfico. Su estudio es importante porque conociendo su
naturaleza, se le puede aprovechar para protegerse de él o beneficiarse
produciendo satisfactores. Ejemplo: Con el estudio de terremotos se han podido
inventar detectores de éstos y medir su rapidez de propagación; con estos
conocimientos y el uso de ondas de radio, se ha logrado alertar poblaciones distantes
del epicentro te un terremoto, que pudieran ser afectadas y así
prevenirse.
El movimiento ondulatorio es una forma de
transmitir energía de un punto a otro a lo largo de un medio elástico, sin
contacto directo entre la fuente generadora y su receptor. El movimiento en el
medio elástico puede ser ocasionado por una perturbación mecánica o una onda
electromagnética, esta ultima puede hacer uso de un medio elástico o no para su
transmisión, como es el caso de la luz proveniente del Sol o de las estrellas;
y la comunicación inalámbrica entre un satélite artificial y una estación en
Para su estudio, los movimientos
ondulatorios los clasificamos en longitudinales y transversales, esta
clasificación está basada en la dirección del desplazamiento del medio y la
dirección de propagación de la energía en forma de ondas. Si las ondas se
propagan en la dirección de desplazamiento del medio se denominan ondas
longitudinales o movimiento ondulatorio longitudinal, ejemplos de estas son las
ondas sonoras en sólidos, líquidos y gases. A continuación ilustramos una onda
acústica (sonora) en un gas.
Figura 72. Onda longitudinal.
Aquí la onda está formada por compresiones
de partículas y rarefacciones de las mismas.
Si el movimiento ondulatorio se propaga
transversalmente a la dirección del desplazamiento del medio, el movimiento se
llama ondulatorio transversal u ondas transversales. Son ejemplos de este
movimiento, las ondas formadas en un estanque al arrojar un objeto; las ondas
en una cuerda fija en sus extremos cuando se le aplica una fuerza hacia arriba;
y las ondas electromagnéticas debidas a la interacción entre dos campos
variables, uno magnético y otro eléctrico. A continuación la ilustración.
Figura 73. Onda transversal.
Para el estudio del movimiento ondulatorio
requerimos conocer el concepto de onda y de algunas definiciones relacionadas
con ésta, como son: frecuencia, período, longitud de onda, velocidad de la
misma, etc.
Onda:
Onda es el conjunto de valores sucesivos
que toma una cantidad de una partícula en movimiento ondulatorio durante un
ciclo. A continuación se ilustra.
Figura 74. Características de una onda.
Onda Electromagnética: Es aquella producto de la interacción de dos campos perpendiculares, uno eléctrico
y el otro magnético, se puede propagar en un medio elástico o en ausencia de
éste. Ejemplo de esta son: ondas de radio, ondas de televisión, microondas,
ondas de luz, etc.
Onda Mecánica: Es la
que aparece en un medio elástico cuando se le perturba aplicándole una presión,
es de frecuencia baja y no se propaga en el vacío.
Elongación y Amplitud: A cada valor de longitud de una onda mecánica, medida perpendicularmente
desde la posición de equilibrio del medio le denominamos elongación, su unidad
de medida es el metro. La elongación mayor de una onda le llamamos Amplitud.
Las elongaciones importantes en una onda son: Cresta, es la amplitud positiva; Nodo es la elongación nula; y Valle que corresponde con la amplitud
negativa.
Semejante a una partícula en M. A. S.
(movimiento armónico simple), la elongación de una partícula en una onda
senoidal se puede determinar para cada instante con el modelo:
Donde A es la amplitud de la onda, X la
elongación y f la frecuencia.
Por lo que respecta a la velocidad
instantánea, el modelo es:
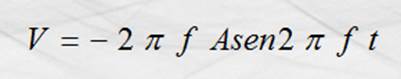
Y la aceleración con el modelo:
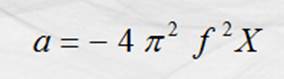
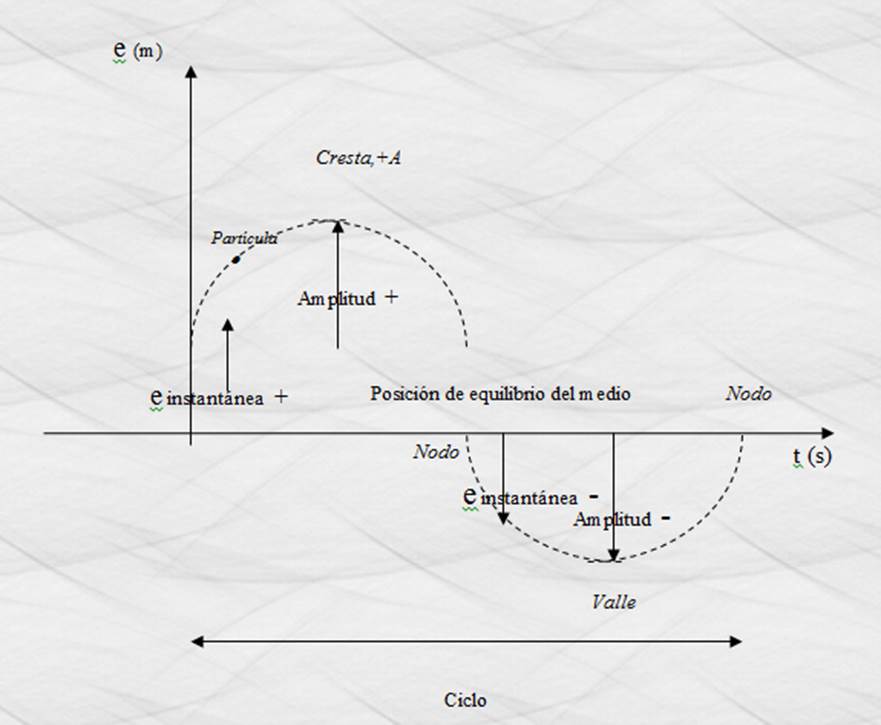
Figura 75. Elongación y amplitud de una
onda.
Si definimos al movimiento ondulatorio en
base a la onda, podemos decir que es un conjunto de ondas sucesivas, cada una
con la misma longitud de onda.
Longitud de onda es la distancia en metros,
entre dos crestas o dos valles consecutivos. La longitud de onda es una
cantidad escalar que tiene como símbolo la letra griega lamda ( l ).
Figura 76. Longitud de onda (l)
Cuando hablamos de movimiento incluimos
implícitamente al tiempo; en el caso de movimientos periódicos como el
ondulatorio, el a armónico simple o el circular uniforme, el tiempo en que se
realiza un ciclo u onda le llamamos periodo, abreviado T y se mide en base al
segundo, en el S. I.
Ya que el movimiento ondulatorio es
repetitivo definiremos como frecuencia al número de ciclos por unidad de
tiempo. Su símbolo es una “f” y la unidad es el ciclo entre segundo, denominado
Hertz, (Hz). Ejemplos de frecuencias son: La frecuencia con que se nos surte la
emergía eléctrica, 60Hz; La frecuencia de los colores que miramos, el verde
amarillo 5.4x 1014 Hz.; el rango de frecuencia audible, 20-20000Hz,
las ondas de radio en F. M. , 88-108 MHz; etc. Por su definición, la frecuencia
resulta la inversa del período y podemos representar esta relación con la
expresión:
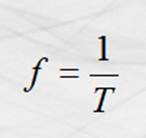
Las ondas poseen rapidez de propagación aun
cuando el medio en el que se propaguen sea pequeño, La rapidez de propagación
de las ondas es constante y se puede determinar dividiendo la distancia
recorrida entre el tiempo empleado; o más propiamente la longitud de onda entre
el período. Matemáticamente:
Y como la frecuencia es la inversa del
período, la velocidad queda:
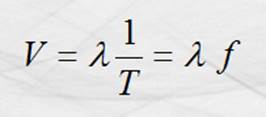
Estas ecuaciones son generales para todas
las ondas y no dependen de la intensidad de la perturbación ni de las
características del medio de propagación. Ahora, citemos ecuaciones de velocidad que si dependen de
las cantidades citadas.
Velocidad de Propagación de una Onda Transversal en una Cuerda:
Se ha comprobado experimentalmente que esta
velocidad depende inversamente de la densidad de masa del medio en que se
propaga y directamente de la magnitud de la perturbación, ejemplo cuando se
propaga una onda transversal en una cuerda, la ecuación para el cálculo de la
velocidad es:
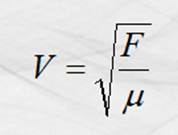
En la que F es la fuerza aplicada a la
cuerda, medida en Newton; m es la densidad lineal de masa de la cuerda
en kg/m; a la vez, la densidad lineal de masa m es la razón aritmética entre la masa de la
cuerda y su longitud.
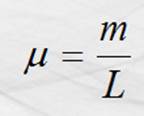
Deducción del modelo:
La figura siguiente muestra que si
aplicamos un impulso a la cuerda igual a F t la cuerda cambiará su cantidad de
movimiento de p0 =
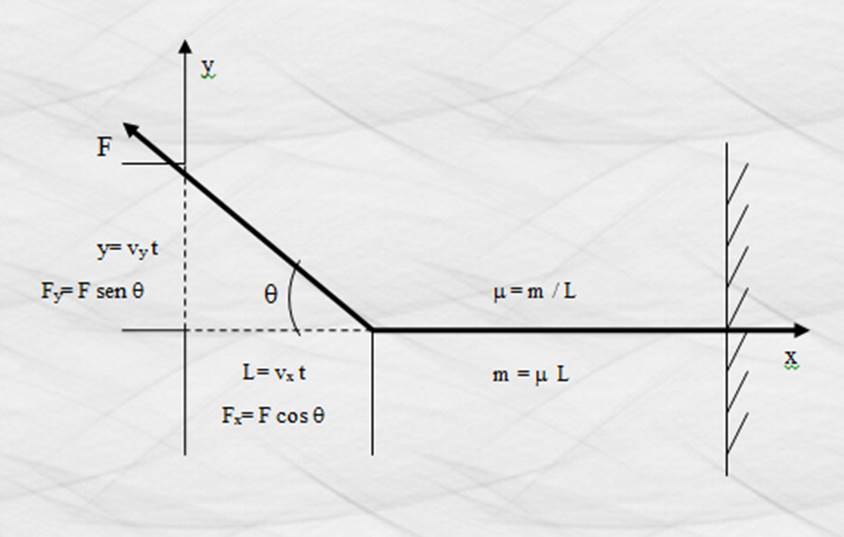
Figura 77. Componentes rectangulares de la
tensión en una cuerda.
Consideraciones:
Para ángulos q pequeños, si q lo medimos en radianes, sen q = q = tg q. m = m L
y como L = vx
t
ya que la onda tiene un movimiento uniforme,
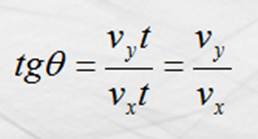
Aplicando al eje y
Impulso = variación de la cantidad de movimiento de m. Y aplicando las
consideraciones propuestas durante el análisis, nos queda:
Fy t = Dpy
F sen q
t = m vy
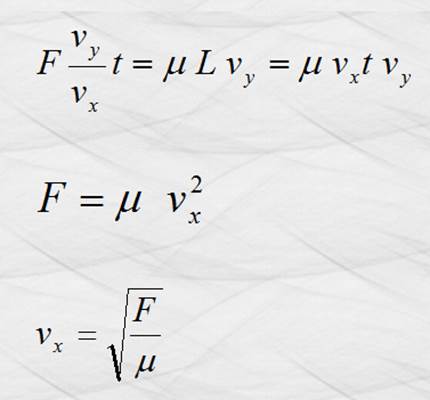
A continuación te mostramos una simulación
de una onda transversal en una cuerda tensa. Aunque está en inglés, aquí te
explicamos como utilizarla: Puedes interactuar con ella, cambiando la tensión
(tension) en la cuerda y el amortiguamiento de la misma (damping).
Sólo agita hacia arriba y hacia abajo el extremo izquierdo de la cuerda (Wiggle wrench!); otra manera de
hacerla funcionar es seleccionar la oscilación automática (Oscillate)
o por pulsos (Pulse). Si deseas reiniciar la simulación, oprime el botón (Restart). El extremo derecho de la cuerda lo puedes dejar
fijo (Fixed End), suelto (Loose End) o imaginar una cuerda
infinita (No End). Intenta todas las posibilidades y
analiza los cambios que surgen en la onda conforme varías los parámetros antes
mencionados.
Energía de una Onda:
Las ondas poseen energía, que es justamente
lo que se transmite.
El modelo de la energía de una onda se
puede determinar de la manera siguiente.
El movimiento ondulatorio se parece al
movimiento armónico simple, de manera
que cada partícula del medio realiza oscilaciones cambiando su energía
cinética a potencial y viceversa, respecto a una posición de equilibrio.
Sabemos que cuando una partícula oscila
respecto de su posición de equilibrio, la energía total en tal posición es
igual a la energía cinética; y la velocidad es máxima, teniendo los modelos
siguientes para estas aseveraciones.
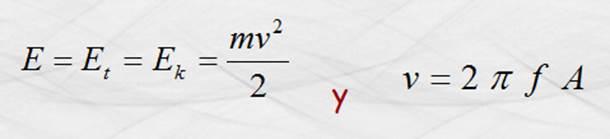
Donde A es la amplitud en metros y f la
frecuencia en Hz.
Sustituyendo la velocidad en la ecuación de la energía
tenemos:
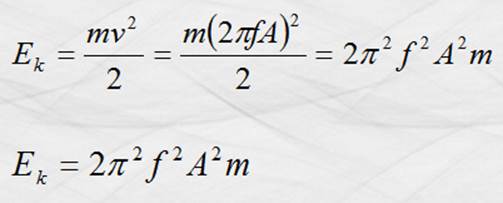
Este es el modelo que representa la energía
de la partícula como de todo el medio elástico, si se considera a “m” como la
masa de la partícula o la del medio.
Rapidez de Propagación de la Energía en la Cuerda o Potencia de la Onda:
De la definición de potencia,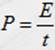 
y sustituyendo
en ésta la E determinada anteriormente, tenemos:
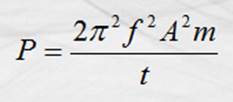
Como la cuerda tiene una densidad lineal de
masa 
y la velocidad para
atravesarla es 
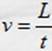, despejando a m y t de
las ecuaciones y sustituyéndolas en la
ecuación de la potencia tenemos:
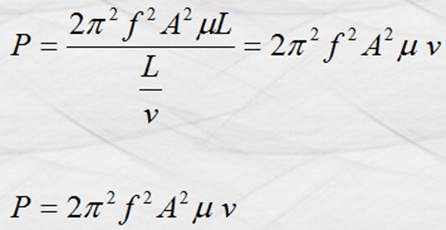
Que como ya dijimos, representa la rapidez
con que la energía se transmite de modo que las unidades resultantes son: 
.
