Teoría Especial de la Relatividad
|
Actividad de Aprendizaje: |
Da a conocer los postulados
de la Teoría Especial de la Relatividad. |
La teoría especial de la relatividad
analiza fenómenos, en los que un observador los visualiza desde un sistema de
referencia que se mueve con velocidad constante, mientras otro los observa
desde otro sistema. Ambos sistemas de referencia se denominan inerciales.

Figura 151. Fenómeno observado desde dos sistemas de referencia
inerciales.
El fenómeno observado por ambos
experimentadores debe ser congruente y las cantidades involucradas, en su
movimiento, deben tener veracidad aunque no concuerden en forma.
Para esta congruencia, Einstein propone los
postulados siguientes:
1.- Todo movimiento es relativo, es
imposible determinar un movimiento absoluto.
2.- La
velocidad de la luz en el vacío es constante independientemente del movimiento
de la fuente y del observador.
Aplicando estos postulados, Einstein obtuvo
una ecuación para conocer cuanto era la longitud calculada desde un sistema en
movimiento rectilíneo uniforme respecto a otro sistema en reposo y es la
siguiente:
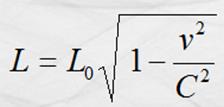
Donde L0 es la longitud medida desde un sistema de coordenadas en
reposo y L es la misma longitud medida desde el sistema de coordenadas en
movimiento rectilíneo uniforme; v la velocidad relativa del observador en
movimiento y C la velocidad de la luz. Esta ecuación representa una contracción
de la longitud vista desde el sistema de coordenadas en movimiento.
A la vez que había reducción de la longitud
de una partícula en movimiento relativo, el tiempo empleado para un evento se
dilataba; lo que expresó de la manera siguiente:
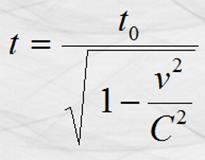
De la misma forma que el tiempo, la masa se
dilataba y el cambio se podía calcular con un modelo semejante que es el
siguiente:
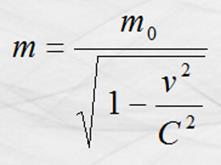
En el que “m” es la masa medida desde el
sistema en movimiento; y m0 la masa medida desde el sistema en
reposo; v la velocidad relativa del observador en movimiento y C la velocidad
de la luz.
Propuso que la masa, aún en reposo, tiene
energía y viceversa. Relacionó a ambas en la ecuación:
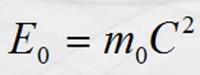
Dedujo una ecuación que relaciona a la
energía cinética y la variación de la masa que es la siguiente:
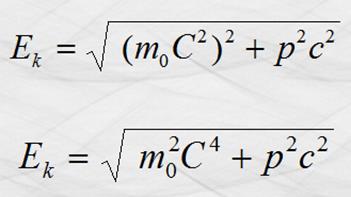
En la que “p” es la cantidad de movimiento
de la partícula. Esta ecuación nos conduce a la siguiente :
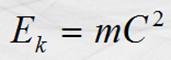
En la que “m” es la masa relativística.
La ecuación más general de la energía
cinética relativística es:
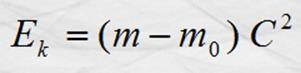
Con
este conjunto de ecuaciones podemos
determinar el comportamiento dinámico de las citadas partículas.
Ve con atención el video siguiente:
|
Crestomatía: Segmento tomado de la serie "Einstein y
la Relatividad Especial", producida por: History Channel, 2003 |